Soal Persamaan dan Pertidaksamaan Rasional dan Irasional - Alysia Kharlotta - X IPS 2

 

Soal Persamaan Rasional

1. Tentukan nilai x yang memenuhi persamaan rasional di bawah ini.

              x + 1    = 2

              x + 2

            A. 10                        C. 5

            B.  3                         D. 15

           Penyelesaian:

            X + 1 = 2 ( X - 2 ) atau X + 1 = 2X - 4

            X - 2X = -4 -1

            -X = -5

            X = 5

          Jawaban:

             C. 5

       2. Tentukan nilai x yang memenuhi persamaan rasional di bawah ini.

             2x - 4   =   4

                X + 1

             A. -4                       C. 10

             B. 4                        D. - 10

         Penyelesaian:

           2X - 4 = 4 (X + 1)

           2X - 4 = 4X + 4 

           2X - 4X = 4 + 4

          -2X = 8

           X = 8/-2 = -4 

         Jawaban:

          A. -4

     3. Tentukan nilai x yang memenuhi persamaan rasional berikut ini:

          X - 3   +     X - 2   = 4

            X - 1      X - 1

        A. 1/2                      C. 3

                B. -3                         D. -1/2

          Penyelesaian:

             X - 3 + (X-2)   = 4

                 X - 1

              2X - 5   = 4

               X - 1

            2X - 5 = 4 (X - 1)

            2X - 5 = 4X - 4

            4X - 2X = -5 + 4

            2X = -1

            X = -1/2

          Jawaban:

            D. -1/2

Soal Pertidaksamaan Rasional

       4.  Pertidaksamaan 2X + 7   <  1 dipenuhi oleh...

                                        X - 1

                 A. 0 < X < 1                 C. -4 < X < 1

                 B. -8 < X  < 1               D. 1 < X < 7

              Penyelesaian:

               2X + 7  <  1

                X - 1

              2X + 7  - 1  <  0

               X - 1     

             2X + 7  - X - 1   <  0

              X - 1      X - 1

             X + 8   <  0

             X - 1

            X = -8

            X = 1

            -8 < X  < 1          

          Jawaban:

            B.  -8 < X  < 1 

     

     5.  Jika    5        >           7      , maka...

                  X - 7             X + 5

        A. X < -5 atau -5 < X < 7.        C. X < -5 atau 7 < X < 37

         B. 7 < X < 37.                            D. -5 < X < 7

     

        Penyelesaian:

          5          _          7       > 0

          X - 7               X + 5

        5 ( X + 5) - 7 (X - 7)   > 0

          ( X - 7 ) ( X + 5 )

        5X + 25 - 7X + 49   > 0

         ( X - 7 ) ( X + 5 )       

            -2X + 74          > 0

         (X - 7) (X + 5)

         X = 37

         X = 7    X = -5

         X < -5 atau 7 < X < 37

        Jawaban:

         C. X < -5 atau 7 < X < 37

 

 6. Himpunan penyelesaian pertidaksamaan

       X^2    <  3X - 2  + 2

      X - 1         X - 1 

     adalah...

     A. { X|X < 1 atau 1 < X < 4 }      C.  { X| -4 < X < -1 }

     B. { X + 1 < X < 4}.                     D. { X|X < 4 } 

     Penyelesaian:

        X^2    _  3X - 2  - 2   < 0

      X - 1         X - 1 

     X^2    _  3X - 2  _ 2X - 2  < 0 

      X - 1         X - 1      X - 1

   X^2 - 3X + 2 - 2X + 2  < 0
           X - 1
   X^2 - 5X + 4  < 0
          X - 1
  ( X - 4 ) ( X - 1)  < 0.       ( X - 1 ) ^2
     ( X - 1 )

  ( X - 4 ) ( x - 1 ) ^2    < 0  

        

     X = 4    X = 1

    X < 1 atau 1 < X < 4

    

    Jawaban:

  

     A. { X|X < 1 atau 1 < X < 4 }

Soal Persamaan Irasional

7. Diketahui persamaan $x-3\sqrt{\frac{5}{x}}=8$ untuk $x>0$. Nilai dari $x-\sqrt{5x}$ adalah $\cdots \cdot$
    A. $2$                       C. $5$                     E. $7$
    B. $3$                       D. $6$

Pembahasan

Dari persamaan $x-3\sqrt{\frac{5}{x}}=8$, kita peroleh
$$\begin{array}{cc}x-8& =3\sqrt{\frac{5}{x}}\\ x-5& =3+3\sqrt{\frac{5}{x}}\\ \text{Kalikan kedua ruas}& \text{dengan}\sqrt{x}\\ (x-5)\sqrt{x}& =3\sqrt{x}+3\sqrt{5}\\ (\sqrt{x}-\sqrt{5})(\sqrt{x}+\sqrt{5})\sqrt{x}& =3(\sqrt{x}+\sqrt{5})\\ (\sqrt{x}-\sqrt{5})\sqrt{x}& =3\\ x-\sqrt{5x}& =3\end{array}$$Jadi, nilai dari $x-\sqrt{5x}=3$
(Jawaban B)

8. Jika $x$ memenuhi $\sqrt{3x-1}=2$, maka nilai dari $x+\frac{1}{3}=\cdots \cdot$
     A. $\frac{1}{3}$                   C. $2$                           E. $3$
     B. $\frac{5}{3}$                   D. $\frac{7}{3}$          

Pembahasan

Diketahui $\sqrt{3x-1}=2$.
Kuadratkan kedua ruas, lalu selesaikan.
$\begin{array}{cc}(\sqrt{3x-1}{)}^2& =2^2\\ 3x-1& =4\\ 3x& =5\\ x& =\frac{5}{3}\end{array}$
Syarat akar:
$3x-1\ge 0\iff x\ge \frac{1}{3}$
Karena $x=\frac{5}{3}$ memenuhi syarat $x\ge \frac{1}{3}$, maka solusi ini diterima.
Jadi, penyelesaian persamaan irasional tersebut adalah $x=\frac{5}{3}$.
Dengan demikian, nilai dari
$x+\frac{1}{3}=\frac{5}{3}+\frac{1}{3}=2$
(Jawaban C)

9. Banyak penyelesaian dari persamaan $\sqrt{x^2-9}=x-3$ adalah $\cdots \cdot$
    A. $0$                        D. $3$
    B. $1$                        E. tak berhingga
    C. $2$

Pembahasan

Diketahui $\sqrt{x^2-9}=x-3$.
Kuadratkan kedua ruas, lalu selesaikan.
$\begin{array}{cc}(\sqrt{x^2-9}{)}^2& =(x-3{)}^2\\ x^2-9& =x^2-6x+9\\ 6x& =18\\ x& =3\end{array}$
Syarat akar $\left(1\right)$:
$\begin{array}{cc}{x}^2-9& \ge 0\\ (x+3)(x-3)& \ge 0\\ x\le -3& \text{atau}x\ge 3\end{array}$
Syarat akar $\left(2\right)$:
$x-3\ge 0\iff x\ge 3$
Perhatikan bahwa $x=3$ memenuhi kedua syarat akar sehingga memenuhi penyelesaian persamaan irasional tersebut. Jadi, hanya ada $1$ penyelesaian persamaan tersebut.
(Jawaban B)

10. Penyelesaian $\sqrt{2x+6}=0$ adalah $\cdots \cdot$
      A. $x=3$                       
      B. $x=-3$                    
      C. $x=0$
      D. $x=-3$ atau $x=3$
      E. $\text{tidak ada}$

Pembahasan

Diketahui $\sqrt{2x+6}=0$.
Kuadratkan kedua ruas, lalu selesaikan.
$\begin{array}{cc}(\sqrt{2x+6}{)}^2& =0^2\\ 2x+6& =0\\ 2x& =-6\\ x& =-3\end{array}$
Syarat akar:
$2x+6\ge 0\iff x\ge -3$
Karena $x=-3$ memenuhi syarat $x\ge -3$, maka solusi ini diterima. Jadi, penyelesaian persamaan irasional tersebut adalah $x=-3$.
(Jawaban B)

Soal Pertidaksamaan Irasional

11. Himpunan semua bilangan real $x$ yang memenuhi $\sqrt{x^2-x-2}<\sqrt{x^2+3x+2}$ adalah $\cdots \cdot$
    A. $x\ge 2$
    B. $x>-1$
    C. $-2\le x\le 1$
    D. $x\le -2$ atau $x\ge 2$
    E. $-2\le x\le -1$ atau $x\ge 2$

Pembahasan

Diketahui $\sqrt{x^2-x-2}<\sqrt{x^2+3x+2}$.
Kuadratkan kedua ruas, lalu selesaikan.
$\begin{array}{cc}(\sqrt{x^2-x-2}{)}^2& <(\sqrt{x^2+3x+2}{)}^2\\ x^2-x-2& <x^2+3x+2\\ -4x& <4\\ x& >-1\left(★\right)\end{array}$
Syarat akar $\left(1\right)$:
$x^2-x-2\ge 0\iff (x+1)(x-2)\ge 0$
Pembuat nol: $x=-1$ atau $x=2$.
Penyelesaiannya adalah $x\le -1\text{atau}x\ge 2$.
Syarat akar $\left(2\right)$:
$x^2+3x+2\ge 0\iff (x+1)(x+2)\ge 0$
Pembuat nol: $x=-1$ atau $x=-2$.
Penyelesaiannya adalah $x\le -2\text{atau}x\ge -1$.
Gunakan garis bilangan.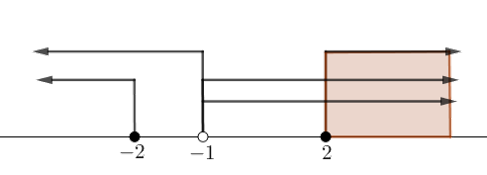

Irisan dari $★$ dan kedua syarat akar di atas merupakan himpunan penyelesaian pertidaksamaan.
Tampak bahwa irisannya adalah $x\ge 2$
(Jawaban A)

$\sqrt{3-5x}>\sqrt{x}$, maka nilai $x$ yang memenuhi adalah $\cdots \cdot$
      A. $x\ge 0$                               D. $0\le x<\frac{1}{2}$
     B. $x<\frac{1}{2}$                              E. $\frac{1}{2}\le x<\frac{3}{5}$
     C. $x\le \frac{3}{5}$

Pembahasan

Diketahui $\sqrt{3-5x}>\sqrt{x}$.
Kuadratkan kedua ruas, lalu selesaikan.
$\begin{array}{cccc}(\sqrt{3-5x}{)}^2& >(\sqrt{x}{)}^2& & \\ 3-5x& >x& & \\ -6x& >-3& & \\ x& <\frac{1}{2}& & \left(★\right)\end{array}$
Syarat akar $\left(1\right)$:
$3-5x\ge 0\iff x\le \frac{3}{5}$
Syarat akar $\left(2\right)$: $x\ge 0$.
Gunakan garis bilangan.

Irisan dari $\left(★\right)$ dan kedua syarat akar di atas merupakan penyelesaian pertidaksamaan.
Tampak bahwa irisannya adalah $0\le x<\frac{1}{2}$
(Jawaban D)

13. Jika $\sqrt{3x-1}<2$, maka nilai $x$ yang memenuhi pertidaksamaan tersebut adalah $\cdots \cdot$
      A. $x<\frac{5}{3}$                          D. $\frac{1}{3}<x<\frac{5}{3}$
     B. $x>\frac{1}{3}$                          E. $\frac{1}{3}<x\le \frac{5}{3}$
     C. $\frac{1}{3}\le x<\frac{5}{3}$

Pembahasan

Diketahui $\sqrt{3x-1}<2$.
Kuadratkan kedua ruas, lalu selesaikan.
$\begin{array}{cccc}(\sqrt{3x-1}{)}^2& <(2{)}^2& & \\ 3x-1& <4& & \\ 3x& <5& & \\ x& <\frac{5}{3}& & \left(★\right)\end{array}$
Syarat akar:
$3x-1\ge 0\iff x\ge \frac{1}{3}$
Gunakan garis bilangan.

Irisan dari $★$ dan syarat akar di atas merupakan penyelesaian pertidaksamaan.
Tampak bahwa irisan dari $\left(1\right)$ dan $\left(2\right)$ adalah $\frac{1}{3}\le x<\frac{5}{3}$
(Jawaban C)