Persamaan dan Pertidaksamaan Rasional - Alysia Kharlotta - X IPS 2 - No. Absen 3


Persamaan dan Pertidaksamaan Rasional

  • Persamaan Rasional
           - Pengertian
                
               Persamaan rasional adalah pecahan dengan satu variabel atau lebih pada bagian pembilang               atau penyebut. Persamaan rasional adalah pecahan apapun yang melibatkan setidaknya satu                    persamaan rasional. Ciri-ciri persamaan rasional ini biasanya tidak mempunyai bentuk akar. 

             Cara menyelesaikan Persamaan Rasional:
                1. Pindahkan semua variabel kesebelah kiri dan yang bukan variabel kesebelah kanan, atau                             sebaliknya (tentunya sesuai aturan matematika).
                2. Tentukan HP (Himpunan Penyelesaian)

         - Contoh Soal Persamaan Rasional     
                1.      x - 5
                       = 2
                            3
                        
                  Cara Penyelesaian :
                 Mengalikan penyebut yang berada di bawah yang bernilai 3 dengan angka 2 yang berada di                    sebelah kanan lalu tulis seperti Ini
                      ×-5= 2.3
                      ×-5= 6
                  lalu kita pindahkan (-5) ke sebelah kanan
                      ×=6+5
                  Kenapa (-5) berubah menjadi 5??
    
                 Karena kalau kita memindah kan melewati tanda =,maka angka tersebut akan berubah                             menjadi lawan angka tersebut.
                     ×=11
           
              2.    x2 - 2x - 8
                      = 0
                        x + 10
                 
               Cara Penyelesaian :
                Pertama kita harus mencari syarat dengan melihat penyebut yang di bawah ×+10 dan di dapat                 syaratnya adalah × tidak boleh sama  dengan -10. Kemudian kita lanjutkan dengan                                 memfaktorkan pembilang (× pangkat 2-2×-8)
                Dan di dapat faktornya yaitu (×+2)(×-4),lalu kita ubah menjadi :
                     ×+2=0          dan         ×-4=0
                     ×=-2                             ×=4

                × kurang dari sama dengan, × lebih dari sama dengan dan × tidak boleh sama dengan -10.


  • Pertidaksamaan Rasional
            - Pengertian
 
                 Pertidaksamaan rasional adalah suatu pertidaksamaan yang bentuknya pecahan atau rasional              dimana penyebutnya memuat suatu variabel.
             Cara menyelesaikan pertidaksamaan rasional:
                1. Ruas kanan jadikan nol
                2. Apabila bisa disederhanakan, maka sederhanakan dulu
                3. Cari pembuat nol untuk pembilang dan penyebut
                4. Buat garis bilangan dan uji tanda positif/ negatif pada interval
                5. Tuliskan HP (Himpunan Penyelesaian)

            - Contoh Soal Pertidaksamaan Rasional
                  1. 

                   Cara Penyelesaian:
                    Langkah awal nyatakan suatu pertidaksamaan diatas dalam bentuk umumnya                                          seperti ini :

                     Karena hasil langkah awal pertidaksamaan tersebut bernilai negatif atau sama                                         dengan nol, maka berlaku sebagai berikut :

 

                    Setelah menentukan irisan pada daerah tersebut, diperoleh bentuk seperti dibawah                                    ini :

                  Dapat disimpulkan dari hasil penyelesaian yang didapat dari pertidaksamaan pada soal                           pertama adalah −13 ≤ x < 4.

                2. 

                   Cara Penyelesaian:

                    Langkah awal nyatakan suatu pertidaksamaan diatas dalam bentuk umumnya seperti                                berikut ini

                   Karena hasil langkah awal pertidaksamaan tersebut sudah bernilai positif atau tidak nol                           hasilnya, maka berlaku sebagai berikut :

                Dapat disimpulkan dari hasil penyelesaian yang didapat dari pertidaksamaan pada soal kedua                 ini adalah −5 < x < −4.

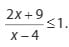
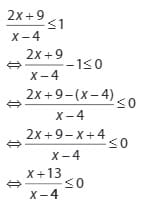
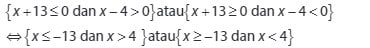
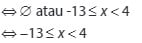
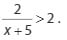
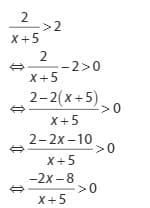
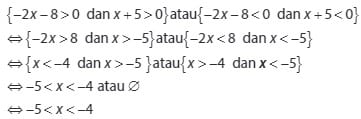
Comments

Post a Comment

Popular posts from this blog

KOORDINAT KUTUB DAN KOORDINAT KARTESIUS

Image
NAMA : ALYSIA KHARLOTTA KELAS : X IPS 2 NO. ABSEN : 03 KOORDINAT KUTUB DAN KOORDINAAT KARTESIUS Koordinat cartesius merupakan suatu titik yang digambar pada sumbu X dan sumbu Y yang biasanya ditulis dengan P(x,y).  Sistem koordinat cartesius juga bisa digunakan pada dimensi lebih tinggi, misalnya  3 dimensi   yang menggunakan sumbu x, y, dan z. Jika pada 2 dimensi digunakan sumbu x dan y, maka sumbu z terletak saling tegak lurus dengan sumbu x dan y.  Koordinat kutub atau koordinat polar merupakan sistem koordinat 2 dimensi, dimana titik bidang ditentukan dari jarak titik yang sudah ditetapkan dan besar sudut ditentukan dari arah yang sudah ditetapkan. Koordinat cartesius dan koordinat kutub serta cara konversi bisa dilakukan dengan menggunakan rumus. Pada gambar tersebut dapat dilihat bahwa koordinat cartesius ditujukan titik P (x,y) dan koordinat kutub P(r,ϑ) dan bisa ditentukan dengan rumus: Jadi, jika diketahui koordinat cartesius P(x,y), maka koordinat kutub bis...
Read more

PENGUKURAN SUDUT

Image
NAMA : ALYSIA KHARLOTTA KELAS : X IPS 2 NO. ABSEN : 03 PENGUKURAN SUDUT Konsep dasar pengukuran sudut adalah membagi satu lingkaran penuh dengan satuan tertentu. Ada tiga pengukuran yang masih banyak digunakan sampai saat ini yaitu : derajat, grad, dan radian. Tetapi yang paling umum dipakai adalah derajat dan radian. Ukuran Derajat Ukuran derajat adalah ukuran yang dapat dibentuk pada bidang datar dengan satuan (°) menggambarkan 1/360 dari putaran penuh. Pada pengukuran sudut dengan derajat ( o ), satu lingkaran penuh adalah 360 o . Seperempat lingkaran atau sudut siku-siku besarnya 90 o , sedangkan sudut lurus adalah 180 o . Ada juga suku yang lebih kecil dari pada derajat, yaitu menit (') , detik (") . Hubungan dari kedua ukuran tersebut  adalah: 1 derajat = 60 menit atau 1° = 60' 1 menit = 60 detik atau 1' = 60" Arah sudut menggunakan arah berlawanan jarum jam bernilai positif dan searah jarum jam bernilai negatif. Karena sangat memudahkan perhitungan pada sa...
Read more